Bootstrapping LLMs for theorem-proving with synthetic data

DeepSeek has created an algorithm that enables an LLM to bootstrap itself by starting with a small dataset of labeled theorem proofs and create increasingly higher quality example to fine-tune itself.

Large language models (LLM) have shown impressive capabilities in mathematical reasoning, but their application in formal theorem proving has been limited by the lack of training data. To address this challenge, researchers from DeepSeek, Sun Yat-sen University, University of Edinburgh, and MBZUAI have developed a novel approach to generate large datasets of synthetic proof data. DeepSeek-Prover, the model trained through this method, achieves state-of-the-art performance on theorem proving benchmarks.

The research shows the power of bootstrapping models through synthetic data and getting them to create their own training data. It can have important implications for applications that require searching over a vast space of possible solutions and have tools to verify the validity of model responses.

The challenges of automatic theorem provers

Automated theorem proving (ATP) is a subfield of mathematical logic and computer science that focuses on developing computer programs to automatically prove or disprove mathematical statements (theorems) within a formal system. 

ATP often requires searching a vast space of possible proofs to verify a theorem. In recent years, several ATP approaches have been developed that combine deep learning and tree search. These models have proven to be much more efficient than brute-force or pure rules-based approaches. But when the space of possible proofs is significantly large, the models are still slow.

A promising direction is the use of large language models (LLM), which have proven to have good reasoning capabilities when trained on large corpora of text and math. However, to solve complex proofs, these models need to be fine-tuned on curated datasets of formal proof languages. But such training data is not available in enough abundance.

To solve this problem, the researchers propose a method for generating extensive Lean 4 proof data from informal mathematical problems. Lean is a functional programming language and interactive theorem prover designed to formalize mathematical proofs and verify their correctness. AI labs such as OpenAI and Meta AI have also used lean in their research.

Generating synthetic proof data

To create their training dataset, the researchers gathered hundreds of thousands of high-school and undergraduate-level mathematical competition problems from the internet, with a focus on algebra, number theory, combinatorics, geometry, and statistics. 

"Despite their apparent simplicity, these problems often involve complex solution techniques, making them excellent candidates for constructing proof data to improve theorem-proving capabilities in Large Language Models (LLMs)," the researchers write.

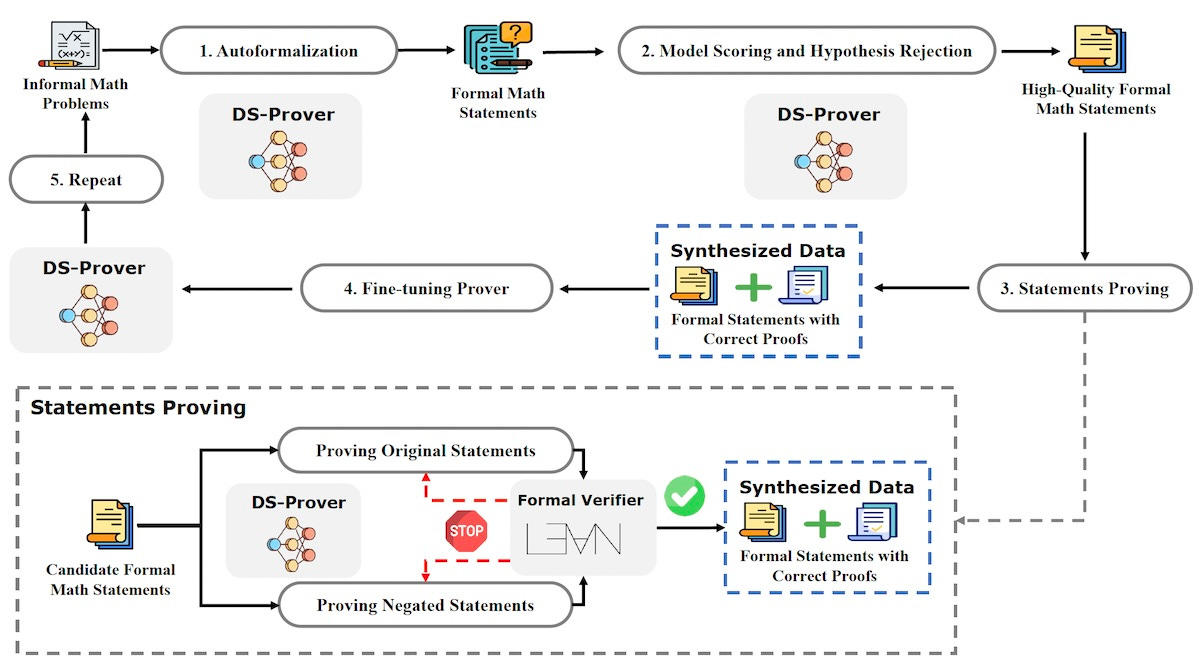
The researchers used an iterative process to generate synthetic proof data. First, they fine-tuned the DeepSeekMath-Base 7B model on a small dataset of formal math problems and their Lean 4 definitions to obtain the initial version of DeepSeek-Prover, their LLM for proving theorems. They used this model to translate the informal math problems into formal mathematical statements in Lean 4.

Next, they used chain-of-thought prompting and in-context learning to configure the model to score the quality of the formal statements it generated. The high-quality examples were then passed to the DeepSeek-Prover model, which tried to generate proofs for them. The proofs were then verified by Lean 4 to ensure their correctness.

To speed up the process, the researchers proved both the original statements and their negations. This method helps to quickly discard the original statement when it is invalid by proving its negation. This reduces the time and computational resources required to verify the search space of the theorems.

The verified theorem-proof pairs were used as synthetic data to fine-tune the DeepSeek-Prover model. The researchers repeated the process several times, each time using the enhanced prover model to generate higher-quality data. They repeated the cycle until the performance gains plateaued.

"Through several iterations, the model trained on large-scale synthetic data becomes significantly more powerful than the originally under-trained LLMs, resulting in higher-quality theorem-proof pairs," the researchers write.

Evaluating DeepSeek-Prover 

The researchers evaluated their model on the Lean 4 miniF2F and FIMO benchmarks, which contain hundreds of mathematical problems. 

On the miniF2F test set, DeepSeek-Prover achieved a whole-proof generation accuracy of 46.3% with 64 samples, surpassing GPT-4 at 23% and a reinforcement learning–based theorem prover at 41%. The cumulative accuracy of DeepSeek-Prover reached 52%.

On the more challenging FIMO benchmark, DeepSeek-Prover solved four out of 148 problems with 100 samples, while GPT-4 solved none. With 4,096 samples, DeepSeek-Prover solved five problems.

"The research presented in this paper has the potential to significantly advance automated theorem proving by leveraging large-scale synthetic proof data generated from informal mathematical problems," the researchers write. 

It also provides a reproducible recipe for creating training pipelines that bootstrap themselves by starting with a small seed of samples and generating higher-quality training examples as the models become more capable. The researchers plan to make the model and the synthetic dataset available to the research community to help further advance the field.

Advancing formal mathematics with LLMs

In an interview with TechTalks, Huajian Xin, lead author of the paper, said that the main motivation behind DeepSeek-Prover was to advance formal mathematics.

"We believe formal theorem proving languages like Lean, which offer rigorous verification, represent the future of mathematics," Xin said, pointing to the growing trend in the mathematical community to use theorem provers to verify complex proofs.

Xin believes that while LLMs have the potential to accelerate the adoption of formal mathematics, their effectiveness is limited by the availability of handcrafted formal proof data. 

"Our goal is to enhance LLM capabilities in formal mathematics through synthetic data, similar to [DeepMind's] AlphaGeometry but with key differences," Xin said. 

AlphaGeometry relies on self-play to generate geometry proofs, while DeepSeek-Prover uses existing mathematical problems and automatically formalizes them into verifiable Lean 4 proofs. AlphaGeometry also uses a geometry-specific language, while DeepSeek-Prover leverages Lean's comprehensive library, which covers diverse areas of mathematics.

"Lean's comprehensive Mathlib library covers diverse areas such as analysis, algebra, geometry, topology, combinatorics, and probability statistics, enabling us to achieve breakthroughs in a more general paradigm," Xin said.

The future of synthetic data and LLMs

Xin believes that synthetic data will play a key role in advancing LLMs. 

"A major concern for the future of LLMs is that human-generated data may not meet the growing demand for high-quality data," Xin said. "Our work demonstrates that, with rigorous evaluation mechanisms like Lean, it is feasible to synthesize large-scale, high-quality data. We aim to show that neural networks and symbolic methods can collaborate in a generative-discriminative manner, promising significant advancements in the era of LLMs, and even towards AGI."

The researchers plan to extend DeepSeek-Prover's knowledge to more advanced mathematical fields.

"Our immediate goal is to develop LLMs with robust theorem-proving capabilities, aiding human mathematicians in formal verification projects, such as the recent project of verifying Fermat's Last Theorem in Lean," Xin said. "To achieve this, we will focus on extending the current data synthesis pipeline to wider and more advanced mathematical fields, rapidly advancing DeepSeek-Prover's knowledge and capabilities."

Read the original paper on Arxiv.