Sampling-based search reveals new LLM scaling laws
Sampling + self-verification can yield impressive results at scale.
We’re still discovering and exploring new scaling laws for AI models. And a new paper by researchers from Google Research and UC Berkeley proposes a simple test-time scaling approach that can boost the reasoning abilities of large language models (LLMs). The technique relies on “sampling-based search,” an algorithm that uses the backbone LLM to generate multiple responses and verify them for correctness. A minimalist implementation of sampling-based search can improve the reasoning performance of non-reasoning LLMs beyond state-of-the-art reasoning models.
The popular method for test-time scaling is to train a model through reinforcement learning to generate chain-of-thought (CoT) traces before emitting the final answer. (This approach is used in OpenAI o3 and DeepSeek-R1.)
Common test-time scaling techniques
RL is efficient but requires heavy investment in training the models, which is beyond the reach of many companies and organizations.
Another popular test-time scaling technique is “self-consistency,” where the model generates multiple responses to the same prompt and chooses the one that shows up more often.
Sampling-based search lets the model generate multiple responses and select the best one through a verification mechanism. The researchers describe sampling-based search as having “the unique advantage of being embarrassingly parallel and allowing for arbitrarily scaling: simply sample more responses.”
Minimalist sampling-based search
In their paper, the researchers propose a minimalist implementation of sampling-based search: The LLM generates the answers and uses “self-verification” to verify its own responses (without relying on ground-truth answers or symbolic verifiers):
1- The model generates N candidates for the prompt. (To generate a diverse set of responses, the researchers use a non-zero temperature setting.)
2- For each answer, the LLM is prompted multiple times to verify its correctness (0 or 1). The average of the verification results becomes the final quality score of the answer.
3- The highest-scored response is selected as the final answer. If multiple candidates are within close range of each other, the algorithm uses pairwise comparison (using the LLM again) to re-evaluate them. The answer with the highest pairwise score is chosen as the final answer.
Sampling-based search can be scaled across two axes: The number of sampled responses and the number of verification steps.
How effective is sampling-based search in action
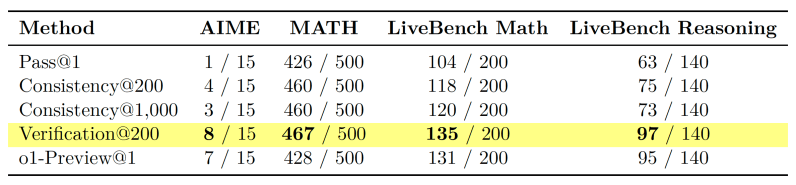
Experiments show that reasoning performance continues to improve with sampling-based search far beyond the point where self-consistency saturates. Even with the minimalist approach of sampling-based search, a model like Gemini 1.5 Pro can surpass o1-Preview on reasoning benchmarks like AIME and MATH.
However, sampling-based search is expensive. For example, with 200 samples and 50 verification steps per answer, a query from AIME can cost up to $650 with Gemini 1.5 Pro (~130 million tokens). This can be mitigated by improving the technique by using more efficient sampling techniques or using smaller models for the verification step. Importantly, sampling-based search is compatible with other test-time scaling methods.
The experiments also reveal two key insights: 1) By directly comparing candidate responses, LLMs can spot disagreements, which hint at mistakes and hallucinations. The researchers describe this as an instance “implicit scaling.” And 2) rewriting the response in task-specific format can improve the quality of the verification stage. For example, verifiers can rewrite candidate responses into a more structured format (e.g., theorem-lemma-proof) before evaluation.
“Given that it complements other test-time compute scaling strategies, is parallelizable and allows for arbitrarily scaling, and admits simple implementations that are demonstrably effective, we expect sampling-based search to play a crucial role as language models are tasked with solving increasingly complex problems with increasingly large compute budgets,” the researchers write.