With test-time scaling, SLMs can beat large language models in reasoning tasks

A small model, a reward model, and a search algorithm can beat an LLM that is 100+ times larger.

A new study by Shanghai AI Laboratory shows that with the test-time scaling (TTS) techniques, an SLM with 1 billion parameters can outperform a 405B LLM on the complex MATH and AIME benchmarks.

Test-time scaling (TTS) is the process of giving LLMs extra compute cylces during inference to improve their performance on various tasks. Leading reasoning models, such as OpenAI o1 and DeepSeek-R1, use “internal TTS,” which means they are trained to “think” slowly by generating a long string of chain-of-thought (CoT) tokens.

The study focuses on “external TTS,” where model reasoning is enhanced with outside help from process reward models (PRMs) and advanced search algorithms such as Monte Carlo Tree Search (MCTS), beam search, and “diverse verifier tree search” (DVTS). External TTS is suitable for repurposing existing models for reasoning tasks without further fine-tuning them.

(Models such as DeepSeek-R1 and OpenAI o3 use “internal TTS,” where the model is trained to generate long chain-of-thought (CoT) sequences instead of using external tools.)

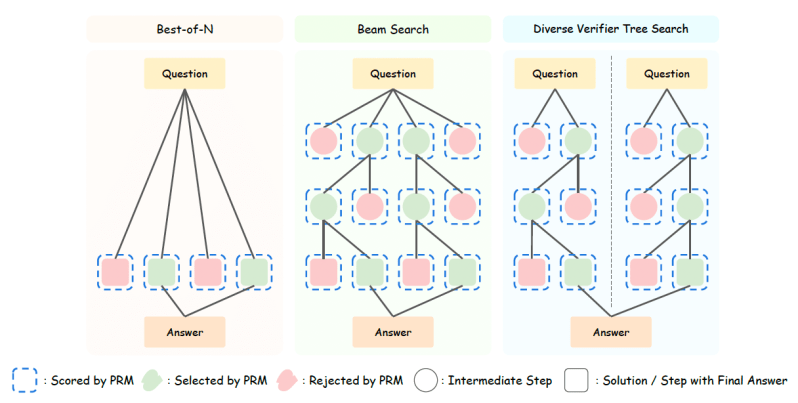
There are various TTS strategies and choosing the best one depends on the specifics of your model and your problem. For example, “best-of-N” is a simple method where the main model (referred to as the “policy model”) generates N answers and the PRM selects one or more best answers to compose the final response. A more advanced setup is to generate several partial answers, rate them through the PRM, and use a beam search algorithm to explore answers that should be further elaborated. The cycle is repeated for multiple rounds until the model generates the complete answer.

The study goes into an in-depth investigation of how different policy models, PRMs, and problem difficulties affect TTS strategies.

Their key findings include the following:

1- The efficiency of TTS strategies is highly dependent on the policy model and PRM. Search-based TTS strategies work better for small policy models, since they don’t have good internal reasoning capabilities. On the other hand, large policy models can get better results from best-of-N because they generate good end-to-end responses and don’t need the guidance of the PRM at every step.

2- Problem difficulty also affects TTS efficiency. For example, for small policy models (fewer than 7B parameters), best-of-N is suitable for easy problems while beam search is better for hard problems. For large policy models (72B+ params), best-of-N is the suitable method for all difficulty levels. (Note that you need to have a model that can classify the difficulty of the problem for this to work.)

The researchers suggest the development of compute-optimal TTS strategies based on policy model, PRM, and problem difficulty.

In their experiments, Llama-3.2-3B model with the compute-optimal TTS strategy outperforms Llama-3.1-405B (135X larger) on MATH-500 and AIME24, two complicated math benchmarks.

Also, Qwen2.5-0.5B outperformed GPT-4o with the right compute-optimal TTS strategy and the 1.5B distilled version of DeepSeek-R1 outperformed o1-preview and o1-mini on MATH-500 and AIME24.

In terms of compute efficiency, SLMs with compute-optimal TTS strategies can outperform larger models with 100-1000X less FLOPS. This is just a reminder of how much juice we can still squeeze out of small language models and test-time scaling laws.